Practical 10 Principal Component Analysis
In biology, shared variation (or "covariance") among variables is very common. In this practical you will learn more about how to implement and interpret Principal Component Analysis, or PCA. Remember, PCA has three benefits to us when dealing with multivariate data:
It can reduce complexity. That is, it provides a way of reducing the number of variables required to describe the data down to fewer variables while still accounting for most of the variation in the recorded variables. This is called "dimension reduction", and is a widely used approach to be able to investigate multivariate data.
It can help to identify interesting biological patterns, including trade-offs and the presence of "latent" factors that are responsible for variation in multiple different variables.
It provides variables that are uncorrelated with one another which can be used in further analyses. In previous weeks, you saw that correlation among predictor variables violates some assumptions of linear models, and can cause uncertainty for hypothesis testing.
In this practical, we will first work with very simple, two-variable data to help you understand what PCA is doing. We will then analyse real data, and lead you through how to interrogate the output to understand the biology captured in that data. In the next practical, you will then use PCA to overcome the limitations of correlations among explanatory variables and test hypotheses.
10.2 Turning our correlated data into uncorrelated data
PCA rotates the data (using matrix algebra that we don't get into in this course) to a new set of uncorrelated axes, and in doing so, converts correlated data into uncorrelated data. Remember: the sequential PCs in PCA are "orthogonal" to one another - which means that they are uncorrelated.
The first step of PCA is to estimate the covariance (or correlation) matrix, and to then subject this to an "eigenanalysis". There are two outputs from this analysis that we need to interpret: The "eigenvalues", which are the variances of each of our new variables and the "eigenvectors", which are our new variables (called "principal components" or PCs). The eigenvectors can also be thought of as the direction of the new axes that we have rotated our data to.
You should recall that from the lecture:
Using the code below, implement the PCA (using the eigen function) on the standardised zebrafish measurements, and then inspect the eigenvalues and eigenvectors (PCs). The following activities will help you understand how to interpret these.
PCA <- eigen(cov_mat) ## Calculate eigenvalues and eigenvectors
round(PCA$values, 3) ## Look at the eigenvalues
round(PCA$vectors, 2) ## Look at the eigenvectors 10.3 Principal Components (Eigenvectors)
The PCs are the key to converting the correlated data into uncorrelated data. Each PC is a list of numbers, which are the loadings, or coefficients that quantify how much each of the original data variables contributes to this new axis.
When we plotted our standardised data above, the position of each point is determined by their Y1 and Y2 values (i.e., where the points fall along the Y1 and Y2 axes). Using these axes as our "coordinate system" to plot the data, we observed that that our variables are highly correlated (~0.8).
The PCs describe a new coordinate system, and when we plot the data on this new coordinate system, we will observe that the "variables" (PCs) are uncorrelated.
First, plot the data again, but this time, let's add the new axes, defined by the eigenvector coefficients (PC loadings):
## Make the plot dimensions square ("s") to help us to visualise the new axes
par(pty = "s")
## Set the range for the two axes
AxisRange <- range(std_data)
## Plot our standardised variables again
plot(x = std_data$TotalLength, y = std_data$TailDepth, ## Plot the two variables
xlim = AxisRange, ## Set the range of Y1 values
ylim = AxisRange, ## Set the range of Y2 values to be identical to the range of Y2 values
xlab = "TotalLength (std)", #label the axes to so you remember what we are plotting
ylab = "TailDepth (std)")
## Now plot straight lines that go through the origin (0, 0)
## and the coordinates of the eigenvectors (one at a time)
## Recall that the slope of a straight line is equal to the rise/run:
abline(0, PCA$vectors[2, 1]/PCA$vectors[1, 1], col = "red") ## Plot a line the for the first PC in red
abline(0, PCA$vectors[2, 2]/PCA$vectors[1, 2], col = "blue") ## Plot a line the for the second PC in blue
## Reset the plot dimensions
par(pty = "m")
Because we standardised TotalLength (Y1) and TailDepth (Y2) to be on the same scale, both the variables have the same variance (1.0), and the data is "centered" on zero. This is convenient for plotting the new PC axes - as you can see, for this data, their origin (where the red and blue lines cross) is in the middle of the data.
How can you tell that, if we plotted the data on our new coordinate axes, that the data will be uncorrelated?
The red and blue lines are perfectly perpendicular (at right angles; AKA they are "orthogonal", just like the Y1 and Y2 axes).
NB: it is easy to see in the plot that the red and blue lines (the PCs) are orthogonal because we made the plot square and the axes identical. If the plot dimensions were not square, or the axes were different, then the PCs may not appear to be perpendicular, but the maths of PCs means they are ALWAYS orthogonal (perpendicular)
What information in the above plot tells us about the relative length of each PC (i.e., the magnitude of their associated eigenvalue)?
The first eigenvector (red line) is associated with the MAXIMUM scatter of points - points fall all along the length of the red line. In contrast, the data is clustered about a the origin of the second eigenvector (the blue line).
10.4 PC scores
The eigenvectors define our new axes, so now let's rotate our data to those new uncorrelated axes. To do this, we calculate the "PC score" for each individual object (in our example, each fish); the object's value for each variable is multiplied by the respective eigenvector coefficient for that variable, and then these products are added together to give the score. For a score on the first PC in our two variable example:
- multiply the Y1 value by the coefficient for Y1;
- multiply the Y2 value by the coefficient for Y2;
- sum the two values.
Go ahead and do this for the first fish in our data. Run each line of code and look at it to follow the three steps:
## Step 1: multiply fish 1's value for Y1 by PC1's loading for Y1
std_data$TotalLength[1] * PCA$vectors[1, 1]
## Step 1: multiply fish 1's value for Y2 by PC1's loading for Y2
std_data$TailDepth[1] * PCA$vectors[2, 1]
## Step 3, sum the two products to calculate the PC1 score for the 1st fish in the dataset
std_data$TotalLength[1] * PCA$vectors[1, 1] + std_data$TailDepth[1] * PCA$vectors[2, 1]Thankfully, we don't have to do this for each eigenvector for each object, R can take care of this using some matrix algebra code (%*% means 'matrix multiply' as we already know from using the curve() function):
PC_scores <- as.matrix(std_data) %*% PCA$vectors ## calculate PC scores for all objects and PCs
colnames(PC_scores)=c("PC1", "PC2")
head(PC_scores) ## Look at the first six objects
## Note: we needed to tell R to treat std_data as a matrix for the "%*%" to workInstead of having TotalLength and TailDepth for each fish, we now have PC1 and PC2 scores for each fish. In other words, instead of having values that define where points fall along the TotalLength and TailDepth axes, the values for each fish now define where points fall along the eigenvectors (the red and blue lines for PC1 and PC2, respectively, that you plotted before).
Our goal was to take a set of correlated values and make them uncorrelated. We now have a new data set, 'PC_scores'. Did it work?
cov_matPCA <- var(PC_scores) ## Calculate the covariance matrix and store it
round(cov_matPCA, 3) ## Look at the variance covariance matrix of PC_scores What is the covariance between the new variables?
Zero; the two variables are completely uncorrelated!
How do the variances of cov_matPCA compare to the eigenvalues of the covariance matrix of simulated data that you analysed (cov_mat)? HINT: you can recall them from your stored R objects to view them: PCA$values.
They are identical! The eigenvalue describes the variance along the eigenvector. The first eigenvalue is large because the points are most spread out along this axis (red line in the plot). Remember, PCA always finds the longest axis first, and then it finds the 2nd longest axis that is uncorrelated to the 1st.
Let's plot the original data side-by-side with the PC data.
Range <- range(std_data, PC_scores) ## Prepare the plotting range
par(mfcol = c(1, 2)) ## Set up space for two graphs, side by side
plot(x = std_data$TotalLength, y = std_data$TailDepth, ## Plot the original data
xlim = Range, ## Set the axes range
ylim = Range, ## Set the axes range
xlab = 'TotalLength', ## Label the vertical axis
ylab = 'TailDepth') ## Label the horizontal axis
plot(PC_scores[, 1], PC_scores[, 2], ## Plot the new data
xlim = Range, ## Set the axes range
ylim = Range, ## Set the axes range
xlab = 'First principal component', ## Label the vertical axis
ylab = 'Second principal component') ## Label the horizontal axis
par(mfcol = c(1, 1)) ## Reset to just one graph per page Compare the two scatter plots.
How did PCA eliminate the correlation between the two variables?
It rotated the data to new axes (PCs) such that the sample covariance was exactly zero. NOTE: while the eigenvalues (i.e., variances of the PCs) will vary depending on the variances and covariances of your original dataset, the covariance bewteen PCS will ALWAYS be zero.
What information in the figure conveys information on the eigenvalues?
The first eigenvector describes the dimension with the MAXIMUM spread on the data (hence, the highest variance);
PC_scores[, 1] are the values for each object along that dimension. The second eigenvector spans a dimension perpendicular to the first; PC_scores[, 2] are values along that dimension. There is much less scatter of points along the second PC (i.e. in the vertical direction) compared to PC1.
Correlated variables are turned into uncorrelated principal component scores by rotating the data. We can demonstrate that no new information has been generated when we perform a PCA. Compare the total variance (referred to as the "trace") of the standardised data, to the total variance in the data after we perform PCA (the sum of the eigenvalues):
## Sum of the variances (i.e. total variance)
## We can grab the variances from the "diagonal" of the covariance matrix!
sum(diag(cov_mat))
## Sum the eigenvalues
PCA$values[1] + PCA$values[2] What tells you that PCA has not generated any new information?
The sum of the variances equals the sum of the eigenvalues.
Which dimension has the least spread of data?
- std_data[, 2]
- PC_scores[, 1]
- std_data[, 1]
- PC_scores[, 2]
- None, the spread is always the same
d. The last principal component (in this case the second) always describes the dimension with the least variance!
10.5 Eigenvector loadings and understanding PC scores
We have converted our Y1 and Y2 variables into PC1 and PC2 variables, but what exactly do these principal components represent?
The key to this question is, again, the eigenvectors. Have a look at the first eigenvector: PCA$vectors[, 1].
There are two numbers. The first number is the coefficient for the first variable (Y1, "TotalLength"), and the second number is the coefficient for the second variable (Y2, "TailDepth"). Two things are important:
The size of the coefficient which tells you about how much a variable contributes to that eigenvector;
The sign (positive/negative) of the coefficient RELATIVE to the other coefficients for that eigenvector. This tells us about whether that variable increases or decreases along the eigenvector.
In our two-variable zebrafish data, PCA$vectors[, 1] has coefficients of Y1 and of Y2 that are ~0.7 (both positive or both negative - we'll return to this point in the box below). PC1 is a variable that represents the positive relationship between Y1 and Y2 (remember: you saw the positive trend and reasonably tight clustering of points along that trend when you plotted the original variables). In this example dataset, we expected both variables to contribute to PC1 (because they share variation with one another!), and we scaled the data so both variables had equal variances (1.0), so we expect Y1 and Y2 to contribute equally.
Let's think about the biological interpretation of PC1 and PC2. PC1 captures the general pattern seen in the correlation between the two variables: as TotalLength increases TailDepth also increases. As such, PC1 can be interpreted as 'size', a composite variable that includes information about length and depth. PC1 is not just some abstract statistical 'variable', it is a new, biologically meaningful variable that we could analyse further.
What might PCA$vectors[, 2] represent? What biological interpretation could you place on PC2?
The coefficients are similar in size, but have opposite signs. That means that PC2 is a variable that describes variation along an axis where Y1 gets larger and Y2 gets smaller (and vice versa). PC2 can be thought of as an 'asymmetry of length and depth' variable.
For our simple zebrafish example, what does it tell you if an individual has an extreme score on PC2?
At one end of PC2 fish are short but have relatively deep tails, and at the other end of PC2, fish are long but have relatively shallow tails. Again, this might be biologically interesting - for example, we might find that males and females differ in the relative depth of their tail, after we account for overall differences in size (PC1).
What do the eigenvalues (PCA$values) tell you? What might be the biological meaning for our zebrafish example?
Most of the spread of the data is along the first eigenvector.
That means that most variation is along an axis that describes overall 'size' (PC1). There is only a little bit of variation associated with 'asymmetry of length and depth' (PC2).
Eigenvector loading signs
Before going any further, we will make one more point about the eigenvectors. It is possible that the eigenvectors from your analysis look different to those of your colleagues, and specifically that they have opposite signs.
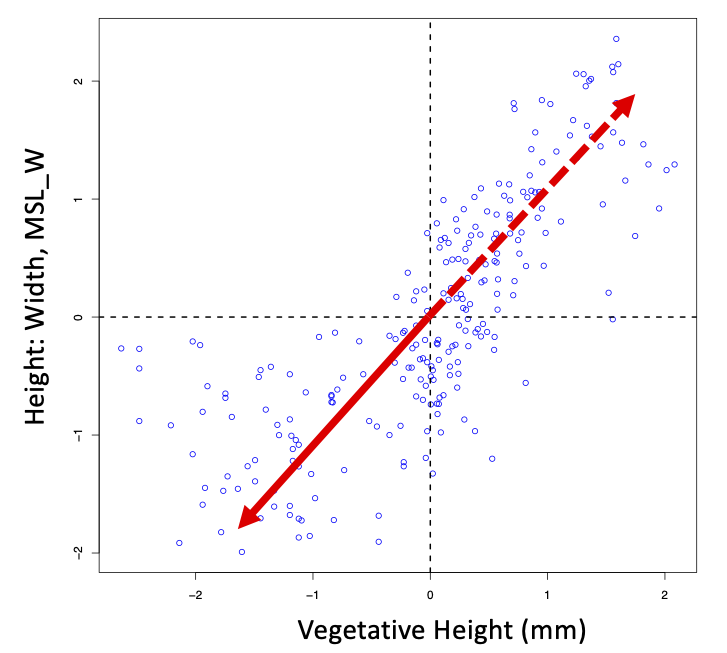
First, recall the plot you made for the standardised data where the average on each axis (i.e., the centre of the axis) was zero. Eigenvectors define the direction from this centre point 0,0, while the eigenvector axis passes through the centroid. It is therefore arbitrary which half of the eigenvector axis the loadings describe. The eigen function in R often returns the vector pointing "down" (all of, or the largest of, the loadings are negative numbers). Because the positive or negative orientation from the centroid is completely arbitrary, we can readily reverse direction along the axis if it is helpful for either interpreting the biology from the loadings, or the ordination of our objects on the axis. We simply multiply the eigenvector by -1.0 (i.e., multiply each variable's loading on that eigenvector by -1 to flip the sign). The figure below illustrates this, where only the first eigenvector is plotted. The solid half of the red arrow (pointing down and left for this example) is where the loadings would be negative, while the dashed half of the arrow (pointing up and right) would be described by positive loadings.
10.6 Summary so far...
Correlation among explanatory variables is problematic for data analysis. By rotating our data to a new co-ordinate system, we can remove correlations, and work with uncorrelated principal components.
We use the eigenvector coefficients to determine what a particular principal component represents, and potentially identify biologically interesting variation (such as asymmetry of length and depth!).
The first principal component always spans the dimension of maximum spread of the data in multivariate space. The second principal component spans the dimension perpendicular (orthogonal) to the first and passes through the next widest spread of the data (for three dimensional data, the third principal component would be perpendicular to both previous axes, and be the third longest axis that meets that criterion of being uncorrelated).
10.7 Zebrafish in four dimensions!!!
Let's explore PCA further through a more thorough analysis of the zebrafish data. These data contain four potential predictor variables of interest that we might want to include in a multiple regression to predict swimming speed:
- fish length ('TotalLength');
- tail depth ('TailDepth');
- body depth ('BodyDepth');
- head length ('HeadLength').
Now that we are no longer dealing with just Y1 and Y2 it is harder to visualise the required four dimensional space, but that is where PCA can help!
These are all measures of fish size and shape, and as you have seen for the first two, we might expect all of them to be correlated to some extent. Have a look:
round(cor(zebrafish[, 6:9]), 3) ## Look at the correlation coefficients
pairs(zebrafish[, 6:9]) ## Observe the pairwise plotsIs there evidence for redundancy among these four variables?
Very likely; the correlations are all very strong, although none are exactly equal to +1 or -1.
Conveniently, there are a number of functions in R (other than eigen()) to perform PCA and visualise the results. Below we use princomp(). We set 'cor=T' to use standardised variables (and hence correlations), rather than the original variables.
## run the PCA
PCA4<-princomp(zebrafish[, 6:9], cor = T)
## look at the loadings
loadings(PCA4)
## Extract the eigenvalues (these are stored as standard deviations instead of variances, so we square them to get variances)
PCA4$sdev^2
## proportion of variance explained by each PC
summary(PCA4)Try running the same PCA without 'cor=T' and compare the results to PCA4. This new PCA will use covariances instead of correlations. It is especially advisable to use correlations when our original variables are measured in different units (e.g., rainfall measured in mm/yr and temperature measured in degrees Celsius).